搜题
2022-10-30 16:46:40 | 来源：网络及考生回忆
13、结合抛掷硬币的试验，简述概率和频率的区别与联系。
三、解答题
14、求线性方程组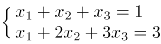
的通解。
四、论述题
15、“几何与代数”是高中数学必修课程内容中的一个主题，该主题的内容包括立体几何、平面解析几何、平面向量、空间向量、复数，试论述：
（1）将“几何与代数”整体设计为一个主题的缘由；
（2）复数与平面向量之间的关系。
五、案例分析题
【材料】
某习题课上有这样一道习题，求函数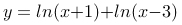
的单调递增区间。
某同学的解法如下：
函数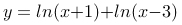
，由于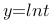
是增函数，所以只需求
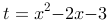的单调性，因为
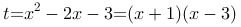，易见该二次函数的单调递增区间为
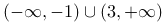。所以函数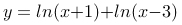的单调递增区间为。
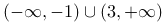16、（1）指出这名学生在求解过程中的错误，并叙述理由；
（2）给出上述题目的正确解答过程。
六、教学设计题
【材料】
下面是某高中数学教材“椭圆及其标准方程”一节的内容片段：
取一条定长的细绳，把它的两端都固定在图板的同一点，套上铅笔，拉紧绳子，移动笔尖，这时笔尖（动点）画出的轨迹是一个圆。如果把细绳的两端拉开一段距离，分别固定在图板的两点
、
（如图所示），套上铅笔，拉紧绳子，移动笔尖，画出的轨迹是什么曲线？
在这一过程中，移动的笔尖（动点）满足的几何条件是什么？
把细绳的两端拉开一段距离，移动笔尖的过程中，细绳的长度保持不变，即笔尖到两个定点的距离的和等于常数。
我们把平面内与两个定点、的距离的和等于常数（大于||）的点的轨迹叫作椭圆（ellipse）。这两个定点叫作椭圆的焦点，两焦点间的距离叫作椭圆的焦距。
由椭圆的定义可知，上述移动的笔尖（动点）画出的轨迹是椭圆。
下面我们根据椭圆的几何特征，选择适当的坐标系，建立椭圆的方程。
17、根据上面的内容，完成下列任务：
（1）写出椭圆标准方程的推导过程（设椭圆的焦距为2c，绳长为2a，焦点在x轴上）；
（2）根据材料设计这部分内容的教学设计，包括教学目标、教学重点、教学过程（含引导学生研究的活动和设计意图）。
注：试题来源于考生回忆及网络，仅供参考！
