2021年4月10日江西省教师招聘考试《小学数学》题

33、有大、小两枚骰子，每枚骰子上的六个面分别画着1~6点，同时抛这两枚骰子，两枚骰子上的数之和为7点的可能性是（  ）。

A、1/6

B、7/36

C、2/9

D、1/4

34、小明从A地到B地的速度为4米/秒，然后又从B地原路以6米/秒的速度返回A地，那么小明在A地与B地之间行一个来回的平均速度为（  ）米/秒。

A、4.2

B、4.8

C、5

D、5.4

35、有5根木条，长度分别为25cm，50cm，75cm，100cm，125cm，从它们当中选出木条拼成一个三角形，一共可以拼成（  ）不同的三角形。

A、4个

B、1个

C、2个

D、3个

36、小明面朝南站立，在体育老师口令下连续六次向左转90度，这时他面朝（  ）。

A、东

B、西

C、南

D、北

37、一双鞋卖160元，要赚60%，卖130元可赚（  ）。

A、60.0%

B、40%

C、30%

D、20%

38、甲、乙两人各走一段路，他们的速度比是3:4，路程比是8:3，那么他们所需时间比是（  ）。

A、2:1

B、32:9

C、1:2

D、4:3

39、一个高30cm的圆锥容器，盛满水倒入和它等底等高的圆柱体容器内，容器口到水面距离是（  ）。

A、20cm

B、15cm

C、30cm

D、10cm

40、从甲、乙两块厚度、边长均相等的正方形钢板上冲制出一些圆形（如图，每块圆形大小分别相同），剩下的边角料质量相比，下面说法正确的是（  ）。

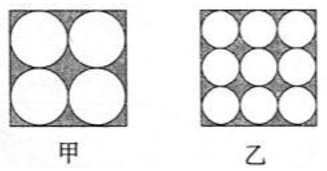
A、甲重

B、乙重

C、质量相等

D、无法确定

41、如图，数轴上被墨水覆盖的数可能是（  ）。

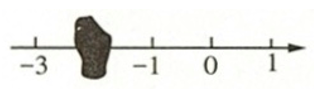
A、-3.2

B、-3

C、-2

D、-0.5

42、第七次人口普查，结果将在4月份向全国公布，我国第六次全国人口普查数据显示，居住在城镇的人口数约666000000人，将其用科学计数法表示为（  ）。

A、66.6*10⁷

B、66.6*10⁸

C、0.666*10⁸

D、6.66*10⁷

43、下列运算中，计算结果正确的是（  ）。

A、x²*x³=x⁶

B、x³+x³=x⁶

C、2(x³)²=x⁶

D、x²ⁿ÷x^n-2=xⁿ⁺²

44、某同学各科成绩如图所示，则其成绩的中位数是（  ）。

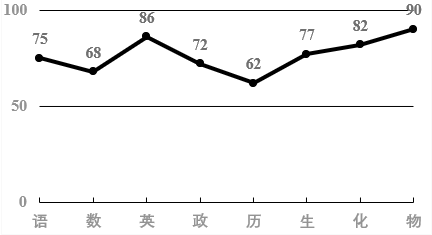
A、75

B、75.5

C、76

D、77

45、图（2）是图（1）中正方体的平面展开图，若正方体上的点A在平面展开图上的位置如图（2）所示，则该正方体

上点B在平面展开图上的位置是（  ）。

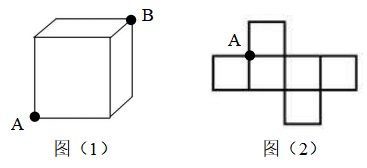
A、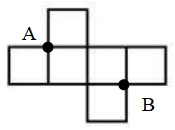

B、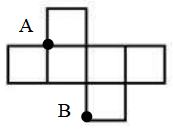

C、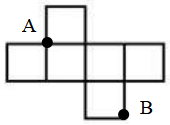

D、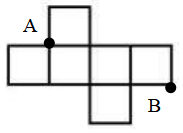

46、如图，在小正方形网格中，ABC的顶点均在网格点上，若点B的坐标是（1，－4），则BC的中点坐标为（  ）。

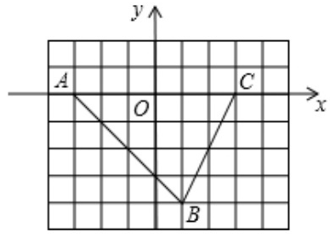
A、（2，－2）

B、（－2，－2）

C、（2，2）

D、（－2，2）

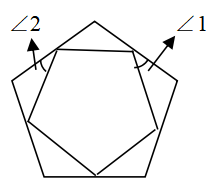
47、两个正五边形按如图所示的方式摆放，若∠1=30°，则

∠2=（  ）。

A、45°

B、42°

C、35°

D、30°

48、关于x的一元二次方程ax²-14x+b=0有两个不相等的实数根，且一个根是另一个根的6倍，则ab=（  ）。

A、7

B、14

C、24

D、28

49、“更相减损术”是出自中国古代数学专著《九章算术》的一种算法，其内容如下：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。”大致意思是：任意给定两个正整数，首先判断它们是否都是偶数。若是，则都除以2；若不是，则以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数，继续这个操作，直到所得的减数和差相等为止。按照这个算法，若给定两个正整数18和42，则最终所得的差为（  ）。

A、21

B、9

C、6

D、3

50、已知某函数的图像C与函数y=3/x的图像关于直线y＝2对称，则下列说法正确的是（  ）。

A、图像C与函数Y=3/x的图像交于点(1,3)

B、点(1/2,-2)在图像C上

C、图像C上的点的纵坐标都小于4

D、若点(x₁，y₁)，(x₂，y₂)，是图像C上的任意两点，若x₁>x₂，则y₁＞y₂

二、简答题。本题满分10分

51、在积极推行农村医疗保险制度以来，某地制定了参加医疗保险的农民医疗费用报销规定。享受医保的农民可在医院就医，在规定的药品品种范围内用药报销比例标准为：500元以下（含500元）不报销，超过500元且不超过10000元的部分报销70%，超过10000元的部分报销80%。请根据以上信息解题：

（1）若甲农民一年的实际医疗费用为11000元，则他按标准可以报销的金额为多少元？

（2）若某农民一年内自付医疗费为5850元，则该农民当年实际医疗费为多少元？

三、解答题。本题满分12分

52、已知二次函数y＝mx2－(3m－1)x－4m＋1与x轴有两个不同的交点A，D（D在A的右边），与y轴交于点C。

（1）求m的取值范围；

（2）证明该二次函数一定经过非坐标轴上的一点B，并求出点B的坐标；

（3）当m＝1时，二次函数在第四象限的图像上是否存在点E，使得△CDE的面积最大，若存在，求出点E的坐标和面积的最大值，若不存在，说明理由。

四、案例分析题。本题满分14分

（一）

材料：

某小学教材中，学习小数乘法选择了以下五个例题。

例1：一个风筝3.5元，买3个风筝多少钱？

例2：0.72×5=

例3：给一个长2.4m，宽0.8m的长方形宣传栏刷油漆，每平方米要用油漆0.9kg，共需要多少kg油漆？

例4：0.56×0.04=

例5：非洲野狗的最高速度是56千米/时，鸵鸟的最高速度是非洲野狗的1.3倍，鸵鸟的最高速度是多少千米/时？

53、（1）依据课标理念，说出每个例题的编写意图。（6分）

（2）结合课标，谈谈在教学中应如何开展小数乘整数的教学？（5分）

（3）结合例题，说一说如何发展学生的运算能力？（3分）

五、教学设计题。本题满分14分

54、以“圆的认识（一）”为例，通过观察、操作、想象等活动，发展学生的空间观念。请你撰写一个教学设计片段，并写出每个教学环节的设计意图。

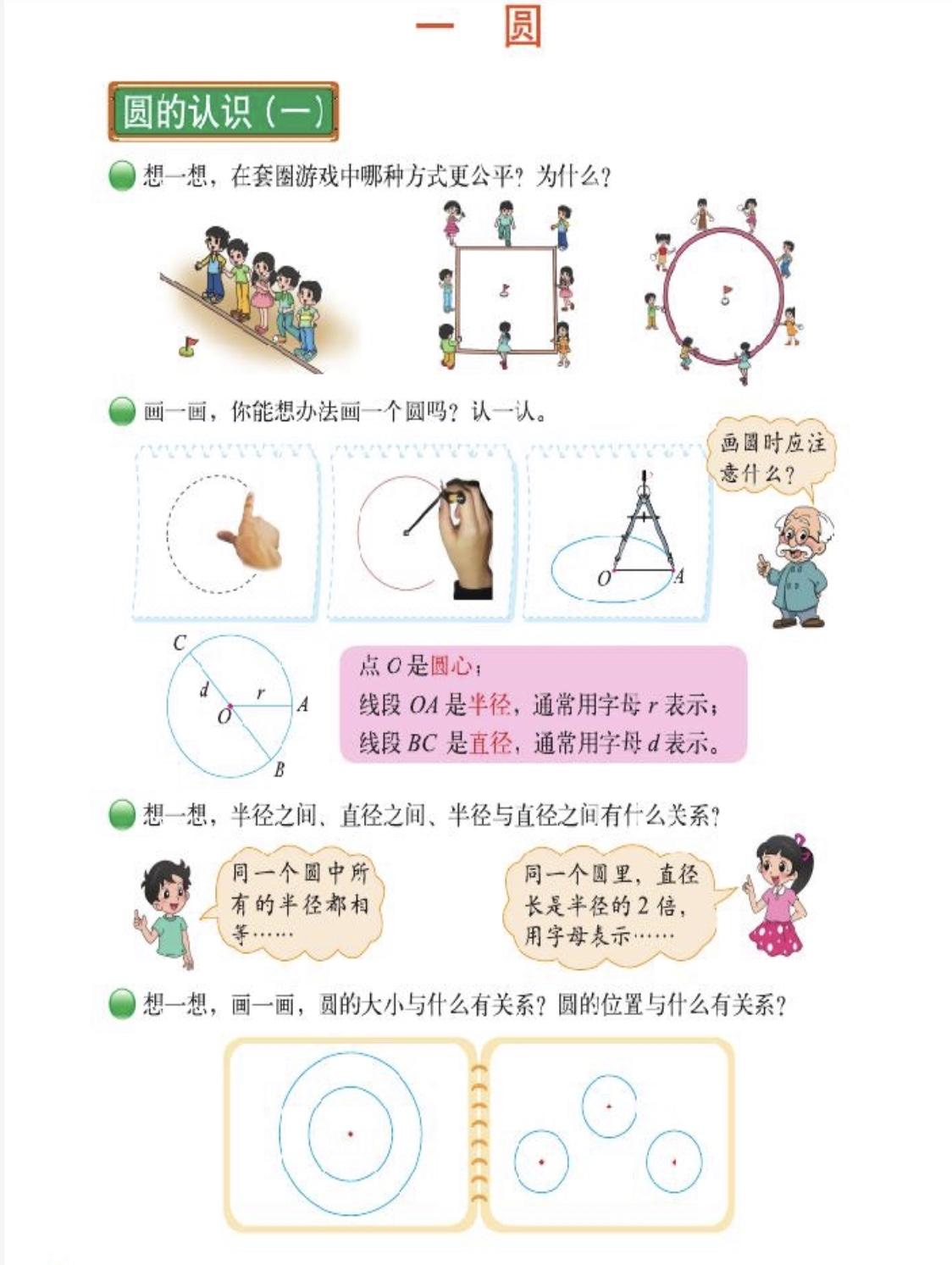
要求：

（1）教学片段要求有层次、有条理。

（2）设计意图要写清楚，每个环节具体落实了哪些“四基”“四能”？

注：试题来源于考生回忆及网络，仅供参考！