2021年4月10日江西省教师招聘考试《初中数学》题

30、如图，在一个米高的楼顶上有一信号塔DC，某同学为了测量信号塔的高度，在地面的A处测得信号塔下端D的仰角为30°，然后他正对塔的方向前进了8米到达地面的B处，又测得信号塔顶端C的仰角为45°，CD⟂AB于点E，E、B、A在一条直线上。信号塔CD的高度为（  ）。

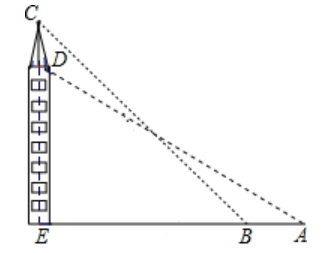
A、20√3

B、20√3-8

C、20√3-28

D、20√3-20

31、对二次函数y=2(x-3)²-4的图象，下列正确的是（  ）。

A、顶点坐标为(-3，-4） 

B、与y轴交点坐标为（0，4）

C、当x≥3时，y随x增大而减小

D、最小值y=-4

32、如图，点A、B、C在正方形网格的格点上，则sin∠ABC（  ）。

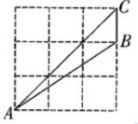
A、√2/6

B、√26/26

C、√26/13

D、√13/13

33、若抛物线y=x²+mx+n的顶点在x轴上，且过点A(a，b）、B（a+6，b），则b的值为（  ）。

A、9

B、6

C、3

D、0

34、下列说法中，不正确的是（  ）。

A、在同圆中，直径是最长的弦

B、在同圆中，所有半径相等

C、圆既是轴对称图形又是中心对称图形

D、长度相等的弧是等弧

35、如图，AB是圆O的直径，EF，EB是圆的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠OFE的度数（  ）。

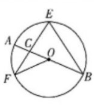
A、30°

B、20°

C、40°

D、35°

36、已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积为（  ）。

A、60πcm²

B、65πcm²

C、120πcm²

D、130πcm²

37、如图，某单位考核情况的条形统计图，（A，B，C三个等级），则下面回答正确的是（  ）。

A、C等级人最少，占总数的30%

B、该单位总共有120人

C、A等级人数比C等级人数多10%

D、等级的人数最多，占总人数的2/3

38、已知圆心O的半径是一元二次方程x²-3x-4=0的一个根，圆心到直线的距离d=6，则直线与圆心O的位置关系（  ）。

A、相离

B、相切

C、相交

D、无法判断

39、反比例函数y=9/x和y=4/x图像如图，点A在y=9/x图像上，连接OA交y=4/x图像与点B，则AB:BO为（  ）。

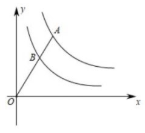
A、1:2

B、2:3

C、4:5

D、4:9

40、如图，在平面直角坐标系中，圆心A的半径为2，圆心坐标为(4,0)，y轴上有点B(0,3)，点C是圆心A上的动点，点P是BC的中点，则OP的范围是（  ）。

A、3/2≤OP≤7/2

B、2≤OP≤4

C、5/2≤OP≤9/2

D、3≤OP≤4

41、命题p：“若x²<1，则x<1”的逆命题是q，则p与q的真假性为（  ）。

A、p真，q真

B、p真，q假

C、p假，q真

D、p假，q假

42、函数的定义域为（  ）。

A、

B、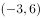

C、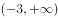

D、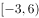

43、下列函数中，既是偶函数又在区间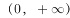上单调递增的是（  ）。

A、y=1/x

B、y=|x|-1

C、y=lgx

D、y=(1/2)^|x|

44、设a，b是两条不同的直线，α，β是两个不同的平面。则a⊥b能得出的是（  ）。

A、a⊥α，b∥β，α⊥β

B、a⊥α，b⊥β，α∥β

C、a⊂α，b⊥β，α∥β

D、a⊂α，b∥β，α⊥β

45、将函数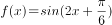的图像向左平移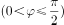个单位长度，所得的图像关于y轴对称，则＝（  ）

A、π/6

B、π/4

C、π/3

D、π/2

46、在ΔABC中，角A，B，C所对的边分别为a，b，c，则b=40，c=20，∠C=60°，则此三角形的解的情况为（  ）。

A、有一解

B、有两解

C、无解

D、有解但解的个数不确定

47、在单调递增的等差数列{a_n}中，若a₃=1，则a₂*a₄=3/4，则a₁=（  ）。

A、-1

B、0

C、1/4

D、1/2

48、设等比数列{a_n}中，前n项和为S_n，已知S₃=8，S₆=7，则a₇+a₈+a₉等于（  ）。

A、57/8

B、-1/8

C、1/8

D、55/8

49、若a<b<0，则下列不等式不能成立的是（  ）。

A、1/(a-b)>1/a

B、1/a>1/b

C、|a|>|b|

D、a²>b²

50、若直线y=kx与圆（x-2）²+y²=1的两个交点关于直线2x+y+b=0对称，则k，b的值分别为（   ）。

A、1/2，-4

B、-1/2，4

C、1/2，4

D、-1/2，-4

二、简答题。本大题一共1小题，每道题目10分，共10分。

51、已知二次函数y=mx²-(3m-1)x-4m+1与轴有两个不同的交点A、D（D在A的右边），与轴交于点C。

（1）求m的取值范围；

（2）证明该二次函数一定经过非坐标轴上的一点B，并求出点B的坐标；

（3）当m=1时，二次函数在第四象限的图像上是否存在点E，使得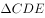的面积最大，若存在，求出点E的坐标和面积的最大值，若不存在，说明理由。

三、解答题。本大题一共1小题，每道题目12分，共12分。

52、如图所示，已知三棱柱ABC-A₁B₁C₁平面A₁ACC₁⟂平面ABC，∠ABC=90°，∠BAC=30°，A₁A=A₁C=AC=2√3，E、F分别是AC、A₁B₁的中点。

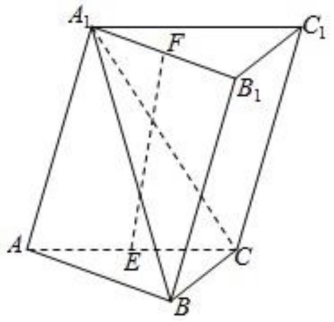
（1）证明：EF⟂BC；

（2）求三棱锥F-ABC的体积。

四、案例分析题。本大题一共1小题，每道题目14分，共14分。

（一）

案例一：“一元一次方程的解法”教学片段

师：解0.5x=1时，先两边除以0.5，把左边变为1x，即x，右边变为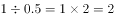，所以。

生1：两边同时乘以2，马上得到，更简单。

师：结果对的，但书上的步骤是两边除以0.5（一次项系数），要按书上格式和要求来。

师：再看一个方程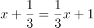：如何解？（思考……）一个学生举手。

生2：老师，不用计算就看出x＝1。

师：光看不行，要按步骤进行计算。接着教师让另一名学生到黑板按书上要求完成了此题，并表扬了这名学生。

案例二：探究“一元二次方程的求根公式”片段

师：对于一般的一元二次方程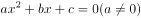

，该如何求解，解的个数情况又是怎样?（学生想到了解方程的所有方法如开平方法、配方法等）

师：我们要研究这样一般的方程的求解方法和解的个数无从下手，该怎么办?

生：举具体例子。

师：非常好！请同桌互相出一个一元二次方程，写解求解过程，并判断根的个数然后小组交流。

探究解方程的通用方法，挑选有代表的予以展示。师生列出方程解的个数情况以及配方法的通用性，并请大家试着用配方法解一元二次方程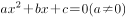

生：我利用配方法导出

的形式，然后该怎么办?（陷入困境）

师：（展示另一个学生的做法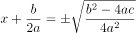）是否正确?

生：不对，应该是。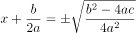

师：很好！还有不同的做法吗?问题的关键在哪?

    ……（师生共同归纳出一元二次方程解的一般情况）

师：请大家快速写出有2个不等实数解，两个相等实数解和无实数解的一元二次方程。 

53、根据以上实例，回答下列问题：

（1）分析案例一中教师处理生1、生2的回答有哪些地方存在不足，面对这种情况你会如何处理？

（2）分析案例二，你认为接下来的重点是什么？难点是什么？这个环节体现了什么数学思想？

（3）结合新课程标准，阐述案例二中教师是如何体现出培养学生的数学创新意识？

五、教学设计题。本大题一共1小题，每道题目14分，共14分。

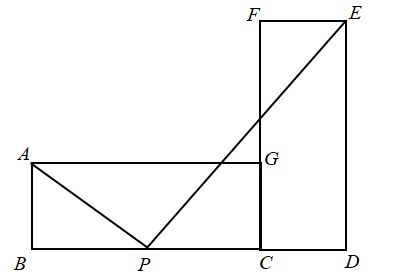
54、如图所示，矩形ABCG（AB<BC）和矩形CDEF全等，点B、C、D在同一条直线上，∠APE的顶点P在线段BD上移动，当点P在什么位置时，使得∠APE为直角？

要求：

（1）撰写解题教学的教学设计；

（2）至少写出三种解题方法的设计及对应环节的设计意图。

注：试题来源于考生回忆及网络，仅供参考！